Where mathematics, insurance and finance meet

Figure 1.  ETHZ building (© Susi Lindig, ETH Zurich, click to enlarge).

Paul Embrechts, Director of RiskLab, outlines some of the current work in finance and insurance in and around RiskLab.

The early days

'Research in Risk Management: Major banks establish a research collaboration. According to a press announcement, the three major banks have founded a common research platform in the field of finance. The aim of this platform is to undertake joint applied research in finance together with relevant universities. A first concrete research contract was made between the Schweizerische Bankgesellschaft (SBG), the Schweizerische Kreditanstalt (SKA), the Schweizerische Bankverein (SBV), and the Swiss Federal Institute of Technology Zurich (ETHZ). Under the name of RiskLab, researchers from the ETH will study concepts, models and techniques from the realm of global risk management and risk monitoring. Every project funded should have a concrete practical question at its basis. Besides other Swiss banks, it is also hoped to get national and international regulatory bodies involved towards the formulation of an appropriate research programme.'

Neue Zürcher Zeitung, 7 October 1994

In the wake of the 1988 BIS Accord, the early 90's saw an intensive discussion on issues such as portfolio effects and netting. By not properly addressing these issues in the 1988 Accord, banks were faced with unsatisfactory risk-based capital rules. Discussions, within industry and with the regulators, led to the 1996 Amendment which became, for instance, mandatory for all US financial institutions with significant trading activities as of 1 January 1998. Notions like marked-to-market, netting, value-at-risk, RAROC became the bread and butter of quantitative risk managers in financial institutions worldwide. At the same time, generally accepted risk principles (GARP) changed the organizational structure of those institutions. For details on this, see Crouchy et al (2001) or www.bis.org.

RiskLab was founded in order to bring an academic component into the discussion between the banks and the regulators on questions related to quantitative risk management. Through the regulatory framework, then (the 1988 Accord, the 1996 Amendment) as well as today (Basel II), it plays an important role in setting the overall research programme and, since the beginning, concrete research proposals have concentrated on specific technical questions. Examples of the latter include the statistical estimation of correlations, an analysis of the square-root scaling rule for VaR and the establishment of risk measures over long-time horizons (e.g. a year). The latter example is one typically encountered in the bank assurance or indeed reinsurance business. It has always been one of the key drivers of ETHZ-based research in risk management to integrate actuarial (insurance) thinking with quantitative (banking related) finance methodology.

Over the years, RiskLab's founding industrial partners changed: two of them merged (SBG and SBV) to become UBS, SKA became part of a larger all-finance group Credit Suisse Group (CSG, also includes the insurance company Winterthur) and the Swiss Reinsurance Company (Swiss Re) joined a little later as a new member. Projects were not only worked on at the ETHZ, but also at the University of Zurich (UNIZH) and the Universities of St. Gallen and Basel. Under its Scientific Director Uwe Schmock, in the late nineties, RiskLab achieved visibility beyond the Swiss boundaries, see www.risklab.ch.

Finance and insurance in Zurich now

One of the other reasons for the industrial support of RiskLab was the desire to make Zurich a truly academic centre of competence of quantitative finance and insurance. This should not only attract top students and academics but also make Zurich a focal point for research and teaching in these fields. The professors that started the RiskLab initiative, Lüthi (operations research) and Embrechts (insurance mathematics), have since been joined at the ETHZ by Delbaen (mathematical finance), McNeil (econometrics), Rheinländer (mathematical finance) and, most recently, Schönbucher (quantitative risk management). A further professorial position is currently being filled in the field of quantitative finance. At the same time, the University of Zurich built up its academic resources in the field through professors Gibson (finance), Hens (financial economics and monetary macroeconomics) and Habib (corporate finance) adding to a strong group of economists already present in Zurich. Excellent quantitative research groups exist at the Institute for Empirical Research in Economics (www.iew.unizh.ch) and the Swiss Banking Institute (www.isb.unizh.ch). Through supervision at the PhD level, these institutes, as well as the Department of Mathematics at the ETHZ, play a fundamental role in safeguarding the academic/scientific component of the research done at RiskLab. Over recent years, teaching and research in finance and insurance has been further enhanced. The University of Zurich, as well as the ETHZ, offers a full teaching programme in actuarial mathematics recognized by the Swiss Actuarial Association (www.actuaries.ch). These programmes lead to the diploma of certified actuary according to the rules of the EU's Groupe Consultatif. From the academic year 2002/2003 onwards, a new Masters Programme in finance has been established jointly by the ETHZ (Department of Mathematics) and the UNIZH (Swiss Banking Institute); see www.msfinance.ethz.ch.

Some RiskLab research projects

I will now discuss some examples of research coming out of RiskLab. Readers interested in more organizational issues, or further details on the numerous RiskLab projects are advised to visit the web page www.risklab.ch/Projects.html. Further information on 'Finance in Zurich' can be found at www.math.ethz.ch/finance and through several links from that page.

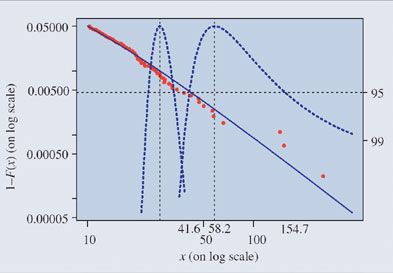1. Figure 2.  EVT analysis of insurance losss data.

   Modelling of extremal events in insurance and finance.
   Together with Claudia Klüppelberg and Thomas Mikosch, I published a book with the above title in 1997 (see Embrechts et al (1997)). Early on it became clear that more and more non-normal based techniques would find their way into financial risk management. Whereas such models were better known to actuaries, finance specialists, for several reasons, had more difficulty in consequently using the technology coming from the realm of extreme value theory (EVT). In Embrechts (2002), these and other actuarial techniques are referred to as insurance analytics. The techniques introduced in this project allow for a better quantile (VaR) estimation in heavy-tailed data. A set of S-plus based programmes for the EVT analysis of finance data (called EVIS) has been worked out by Alexander McNeil; see www.math.ethz.ch/~mcneil/software.html.
         A typical example of an EVT analysis of (insurance) loss data is to be found in figure 2. For more details underlying the analysis of these data, see McNeil (2000).
   
2. Coherent risk measurement.
   In parallel to the above project, researchers working with Delbaen and Artzner (visiting professor of RiskLab) established the, by now fundamental, theory of coherent risk measures; see Artzner et al (1999). Out of this theory, and related work in RiskLab, it followed that pure quantile risk measures are insufficient for proper risk measurement and capital allocation. Measures 'beyond VaR' have now become widely accepted in the industry. RiskLab made several fundamental contributions to this field of research including work on portfolio optimization under coherent risk measure constraints. Current work in this area concentrates on multiperiod coherent risk measurement and applications of game theoretic concepts to coherent capital allocation.
3. Copulae.
   Through the contact of RiskLab researchers with risk managers from industry it became clear that simulation methodology for portfolios with non-normally distributed profit-and-loss distributions was an issue. In addition, the further development of integrated risk management needed aggregation results for several, possibly non-coherent, risk measures. From these questions, a project was formulated analysing the measures of dependence beyond linear correlation. See figure 3 for a warning on a naive application of correlations.
         Around 1997, the already well-known notion, in the world of statistics, of copulae, was introduced to the field of quantitative risk management. For a discussion of the results developed in that period, see Embrechts et al (1999) and Embrechts et al (2002). Techniques developed in this project allow for stress testing portfolios beyond normality both at the levels of the marginal risk factors and at the level of the dependence structure. Other applications include default dependence in credit risk management and the estimation of the degree of non-subadditivity of value-at-risk for non-elliptical portfolios.

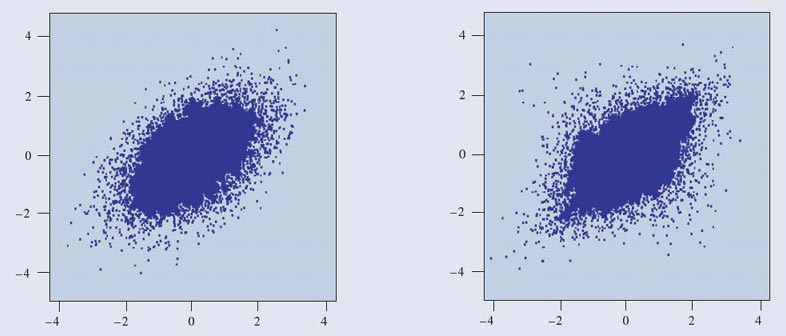   Figure 3.  Two portfolios, both with standard normal margins, correlation 50% but different copulae: a normal copula for the left picture, a t4 copula for the right one.

   
   
4. Current work
   very much concentrates on the modelling of operational and credit risk in the light of Basel II. These problems are studied at the methodological as well as at the applied level, the latter by, for instance, calibrating the models analysed to Swiss market data. In addition, RiskLab concentrates on computational issues through professors Lüthi (operations research) and Schwab (numerical analysis). For example, efficient computation of multiperiod risk measures (for the former) and fast deterministic computation of valuations for assets driven by Lévy processes (for the latter). A further development concerns the applications of financial risk management methodology to general corporations. The main problems discussed at the Institute of Operations Research of the ETHZ (IFOR: www.ifor.math.ethz.ch) concern the valuation of real options and hedging strategies for electricity contract engineering.

Conclusion

Since its start in 1994, RiskLab has evolved with and within the world of banking and insurance. One constant that has remained is the idea of precompetitive research together with sponsoring partners from industry. No doubt, RiskLab will need to find its optimal position among the, by now, extensive offer of teaching and research in insurance and finance in Zurich and more generally in Switzerland. After the recent upheavals in financial markets more, not less, quantitative thinking concerning best practice risk management methodology is needed. It is certain that RiskLab, in one form or another, will keep on playing an important and internationally visible role in this discussion. At least one proof of its success is that its concept was copied on several occasions in other countries, as a Google search will quickly reveal.

References

1. P. Artzner, F. Delbaen, J.-M. Eber and D. Heath (1999) Coherent measures of risk, Math. Finance 9, pp. 203–28
2. M. Crouchy, D. Galai and R. Mark (2001) Risk Management (New York: McGraw-Hill).
3. P. Embrechts (2002) Insurance analytics (Guest Editorial) British Actuarial J., at press.
4. P. Embrechts, C. Klüppelberg and T. Mikosch (1997) Modelling Extremal Events for Insurance and Finance (Berlin: Springer).
5. P. Embrechts, A. McNeil and D. Straumann (1999) Correlation: pitfalls and alternatives, Risk 5, pp. 69–71.
6. P. Embrechts, A. McNeil and D. Straumann (2002) Correlation and dependence in risk management: properties and pitfalls, Risk Management: Value at Risk and Beyond, ed. M. A. H. Dempster (Cambridge: Cambridge University Press) pp. 176–223.
7. A. McNeil (2000) Extreme value theory for risk managers, Extremes and Integrated Risk Management, ed. P. Embrechts (London: Risk Books) pp. 3–18.

Paul Embrechts, Director of RiskLab

Please send comments and suggestions to Uwe Schmock, email: schmock@math.ethz.ch. Last update: February 15, 2003